KMP字符串

AcWing 831. 字符串查找—用16幅图从暴力一步步优化到KMP – AcWing

/*
给定一个字符串 S，以及一个模式串 P，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模式串 P 在字符串 S 中多次作为子串出现。

求出模式串 P 在字符串 S 中所有出现的位置的起始下标。

输入格式
第一行输入整数 N，表示字符串 P 的长度。

第二行输入字符串 P

第三行输入整数 M，表示字符串 S 的长度。

第四行输入字符串 S

输出格式
共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。

数据范围
1≤N≤10^5

1≤M≤10^6

输入样例：
3
aba
5
ababa
输出样例：
0 2
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10,M = 1e6+10;
int p[N],s[M];
int ne[N];
int main(){
    int n,m;
    string p,s;//模式串p，字符串s，下标从0开始的
    cin>>n>>p>>m>>s;
    for(int i=1,j=0;i<n;i++){
        while(j && p[i]!=p[j])j=ne[j-1];//j要减一
        if(p[i]==p[j])j++;
        ne[i]=j;
    }
    // for(int i=0;i<n;i++){
    //     cout<<ne[i]<<" ";
    // }
    for(int i=0,j=0;i<m;i++){
        while(j && p[j]!=s[i])j=ne[j-1];
        if(p[j]==s[i])j++;
        if(j==n){
            cout<<i-j+1<<" ";
            j=ne[j-1];
        }
    }
    return 0;
}

以下是 j = ne[ j – 1 ] 的原因

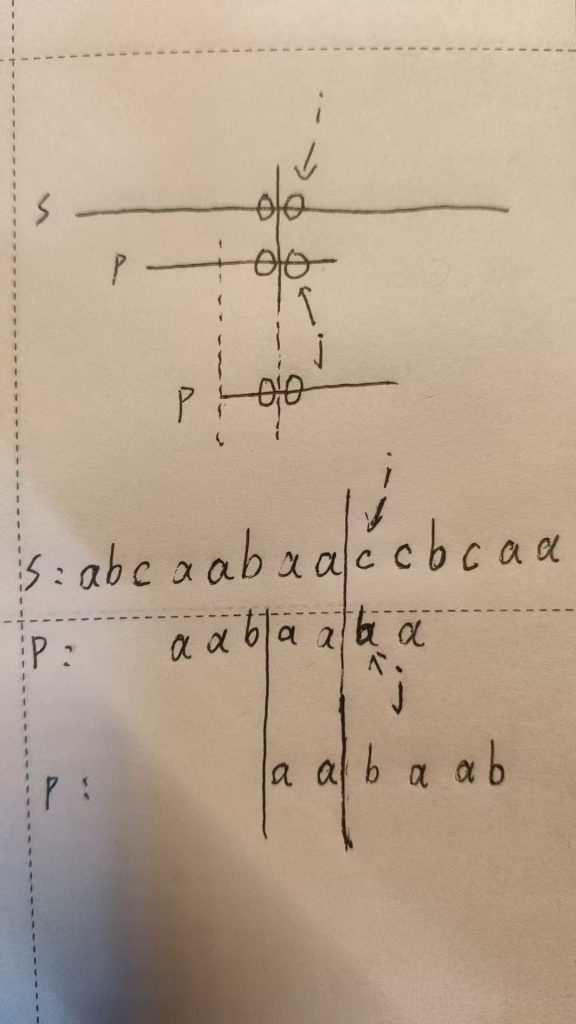
Trie字符串统计

AcWing 835. Trie树图文详解 – AcWing

/*
维护一个字符串集合，支持两种操作：

I x 向集合中插入一个字符串 x；
Q x 询问一个字符串在集合中出现了多少次。
共有 N 个操作，所有输入的字符串总长度不超过 105，字符串仅包含小写英文字母。

输入格式
第一行包含整数 N，表示操作数。

接下来 N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式
对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x 在集合中出现的次数。

每个结果占一行。

数据范围
1≤N≤2∗104

输入样例：
5
I abc
Q abc
Q ab
I ab
Q ab
输出样例：
1
0
1
*/
//如果只是统计个数的话我感觉还是map数组更方便，但是这题主要学习的是Trie树，所以尽量还是用trie树
//用map的做法
#include<bits/stdc++.h>
using namespace std;
map<string,int>s;
int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        char c;
        cin>>c;
        if(c=='I'){
            string a;
            cin>>a;
            s[a]++;
        }else if(c=='Q'){
            string a;
            cin>>a;
            int sum=0;
            for(auto it:s){
                if(it.first==a)sum+=it.second;
            }
            cout<<sum<<endl;
        }
    }
    return 0;
}
//用trie树的做法
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int son[N][26],idx;
int cnt[N];

void insert(string s){
    int p=0;
    for(int i=0;i<s.size();i++){
        int a = s[i]-'a';
        if(!son[p][a]){
            son[p][a] = ++idx;
        }
        p = son[p][a];
    }
    cnt[p]++;
}

int query(string s){
    int p = 0;
    for(int i=0;i<s.size();i++){
        int a = s[i]-'a';
        if(!son[p][a])return 0;
        p = son[p][a];
    }
    return cnt[p];
}
int main(){
    int n;
    cin>>n;
    while(n--){
        char c;
        string s;
        cin>>c>>s;
        if(c=='I'){
            insert(s);
        }else {
            cout<<query(s)<<endl;
        }
    }
    return 0;
}

最大异或对

AcWing 143. 最大异或对—Trie详解 – AcWing

/*
在给定的 N 个整数 A1，A2……AN 中选出两个进行 xor（异或）运算，得到的结果最大是多少？

输入格式
第一行输入一个整数 N。

第二行输入 N 个整数 A1～AN。

输出格式
输出一个整数表示答案。

数据范围
1≤N≤10^5
0≤Ai<2^31

输入样例：
3
1 2 3
输出样例：
3
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int son[N*31][2];
int idx,ret;
void insert(int a){
    int p = 0;
    for(int i=30;i>=0;i--){
        int u = a >> i & 1;
        if(!son[p][u]){
            son[p][u]=++idx;
        }
        p=son[p][u];
    }
}
int quary(int a){
    int p = 0;
    int sum=0;
    for(int i=30;i>=0;i--){
        int u = a >> i & 1;
        if(son[p][!u]){
            p = son[p][!u];
            sum = sum * 2 + !u;
        }else{
            p = son[p][u];
            sum = sum * 2 + u;
        }
    }
    return a^sum;
}
int main(){
    int n,maxx=0;
    cin>>n;
    while(n--){
        int a;
        cin>>a;
        insert(a);
        maxx = max(maxx,quary(a));
    }
    cout<<maxx<<endl;
    return 0;
}

将数转换成二进制存储到trie树中，异或运算时相异为真、相同为假，所以在固定一个数后尽可能找跟原来的数的二进制的每一位相异的数，之后求出他们的异或运算后的值，这是以当前数为固定值的最大的异或值，然后找出其中最大的输出