一种将大范围的数据映射到一个小范围的数据结构,将大范围压缩到一个小范围会有冲突的问题,比如两个不同的值映射到了同一个下标,因此右两种处理冲突的方法,分别是拉链法、开放寻址法
拉链法
对于一组数据定义一个一维数组,对数据依次进行哈希然后存到对应下标,如果当前下标已经有数据了就将新值接到旧值上面,使用邻接表存储
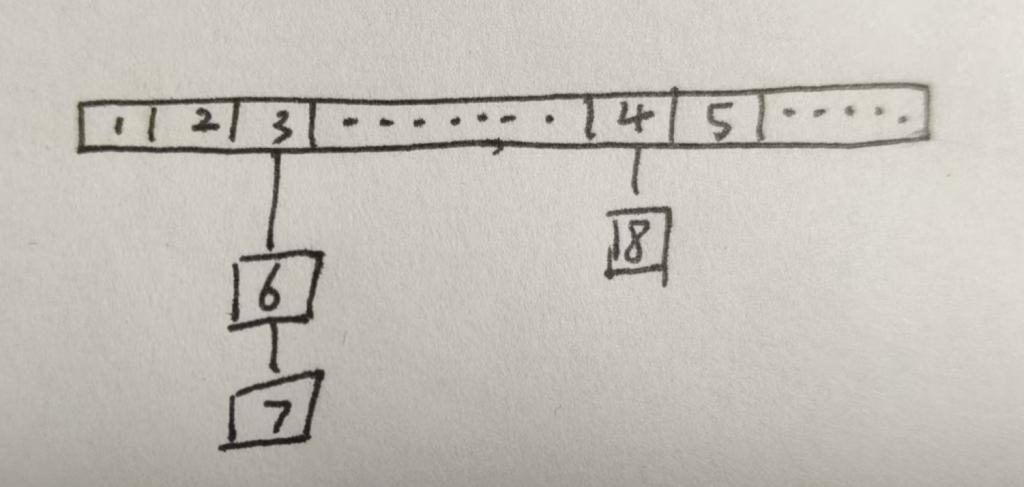
拉链法模板
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5+10;
int h[N],e[N],ne[N],idx;//邻接表存储
void insert(int x){
int k = (x%N+N)%N;//避免余数为负数
e[idx] = x;
ne[idx] = h[k];
h[k] = idx++;
}
bool find(int x){
int k = (x%N+N)%N;
for(int i=h[k];i!=-1;i=ne[i]){
if(e[i]==x)return true;
}
return false;
}
int main(){
memset(h,-1,sizeof h);
int n;
cin>>n;
while(n--){
string s;
int x;
cin>>s>>x;
if(s=="I"){
insert(x);
}else if(s=="Q"){
if(find(x))cout<<"Yes\n";
else cout<<"No\n";
}
}
return 0;
}开放寻址法
对于一组数据定义一个一维数组,对数据依次进行哈希然后存到对应下标,如果当前下标已经有数据了就往后面找,找到的第一个空元素将值存进去
开放寻址法模板
#include<iostream>
#include<cstring>
using namespace std;
const int N = 2e5+3;//最大一共有1e5个不同的数据,考虑到冲突的情况直接定义两倍
const int null = 0x3f3f3f3f;//规定空指针为0x3f3f3f3f
int h[N];
int find(int x){//查找值x映射到的下标
int k = (x%N+N)%N;
while(h[k]!=null && h[k]!=x){
k++;
if(k==N){
k=0;
}
}
return k;
}
int main(){
memset(h,0x3f,sizeof h);//初始都为空
int n;
cin>>n;
while(n--){
string s;
int x;
cin>>s>>x;
if(s=="I"){
h[find(x)]=x;
}else if(s=="Q"){
if(h[find(x)]==null)cout<<"No\n";
else cout<<"Yes\n";
}
}
return 0;
}
模拟散列表
维护一个集合,支持如下几种操作:
I x,插入一个整数 xx;Q x,询问整数 xx 是否在集合中出现过;
现在要进行 NN 次操作,对于每个询问操作输出对应的结果。
输入格式
第一行包含整数 NN,表示操作数量。
接下来 NN 行,每行包含一个操作指令,操作指令为 I x,Q x 中的一种。
输出格式
对于每个询问指令 Q x,输出一个询问结果,如果 xx 在集合中出现过,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤N≤105
−109≤x≤109
输入样例:
5
I 1
I 2
I 3
Q 2
Q 5
输出样例:
Yes
No//开放寻址法
#include<iostream>
#include<cstring>
using namespace std;
const int N = 2e5+3;//最大一共有1e5个不同的数据,考虑到冲突的情况直接定义两倍
const int null = 0x3f3f3f3f;//规定空指针为0x3f3f3f3f
int h[N];
int find(int x){//查找值x映射到的下标
int k = (x%N+N)%N;
while(h[k]!=null && h[k]!=x){
k++;
if(k==N){
k=0;
}
}
return k;
}
int main(){
memset(h,0x3f,sizeof h);//初始都为空
int n;
cin>>n;
while(n--){
string s;
int x;
cin>>s>>x;
if(s=="I"){
h[find(x)]=x;
}else if(s=="Q"){
if(h[find(x)]==null)cout<<"No\n";
else cout<<"Yes\n";
}
}
return 0;
}
//拉链法
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5+10;
int h[N],e[N],ne[N],idx;//邻接表存储
void insert(int x){
int k = (x%N+N)%N;//避免余数为负数
e[idx] = x;
ne[idx] = h[k];
h[k] = idx++;
}
bool find(int x){
int k = (x%N+N)%N;
for(int i=h[k];i!=-1;i=ne[i]){
if(e[i]==x)return true;
}
return false;
}
int main(){
memset(h,-1,sizeof h);
int n;
cin>>n;
while(n--){
string s;
int x;
cin>>s>>x;
if(s=="I"){
insert(x);
}else if(s=="Q"){
if(find(x))cout<<"Yes\n";
else cout<<"No\n";
}
}
return 0;
}字符串哈希
对一个字符串求出前缀哈希值,方便进行区间判断,哈希算法是将字符看成一个P进制的数,并且当P为131或13331,值对Q(264)取余时,可以理解为不存在冲突的情况
其中unsigned long long的最大值为264-1,如果溢出就相当于对264取余
例题
给定一个长度为 nn 的字符串,再给定 mm 个询问,每个询问包含四个整数 l1,r1,l2,r2l1,r1,l2,r2,请你判断 [l1,r1][l1,r1] 和 [l2,r2][l2,r2] 这两个区间所包含的字符串子串是否完全相同。
字符串中只包含大小写英文字母和数字。
输入格式
第一行包含整数 nn 和 mm,表示字符串长度和询问次数。
第二行包含一个长度为 nn 的字符串,字符串中只包含大小写英文字母和数字。
接下来 mm 行,每行包含四个整数 l1,r1,l2,r2l1,r1,l2,r2,表示一次询问所涉及的两个区间。
注意,字符串的位置从 11 开始编号。
输出格式
对于每个询问输出一个结果,如果两个字符串子串完全相同则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤1051≤n,m≤105
输入样例:
8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2
输出样例:
Yes
No
Yes#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;//直接用unsigned long long
const int N = 1e5+10;
const int P = 131;
ll h[N],p[N];
int main(){
int n,m;
cin>>n>>m;
string s;
cin>>s;
s=" "+s;
h[0]=0;
p[0]=1;
for(int i=1;i<=n;i++){
h[i]=h[i-1]*P+s[i];
p[i]=p[i-1]*P;
}
while(m--){
int l1,r1,l2,r2;
cin>>l1>>r1>>l2>>r2;
if((h[r1]-h[l1-1]*p[r1-l1+1])==(h[r2]-h[l2-1]*p[r2-l2+1]))cout<<"Yes\n";
else cout<<"No\n";
}
return 0;
}